第6回目の理論記事では機械学習におけるデータの前処理の重要性を'16 フェブラリーSの予測を交えて説明します。
入力データの大きさを整える
前回の理論記事で特徴量には数値データとカテゴリデータがあることをお話しました。カテゴリデータはダミー変数に変換してしまえば0か1のいずれかの値となりますが、数値データはコース距離や本賞金といった大きなスケールの値を取る場合があります。そのようなデータの範囲が大きく異なる特徴量が特徴ベクトルに含まれると、パラメータの更新がうまくいかなかったり、値の大きな特徴量だけが結果に寄与するような予測器ができてしまいます。中には決定木などスケールに影響されないアルゴリズムもありますが、多くの機械学習のアルゴリズムではスケールを適切に調整した方が良い結果となります。
よく使われるスケーリング手法は*正規化(normalization)と標準化(standarization)*です。正規化は文脈によって意味が異なりますが、多くの場面においては特徴量のとる範囲を[0, 1]に変換することを指します。正規化はあらかじめ特徴量のとりうる値の範囲が決められているときに有効です。以下の線形変換により正規化がされます。
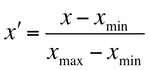
一方標準化では特徴量の分布を平均0、分散1になるように変換します。標準化は正規化のように上下限を設定していないため、外れ値が存在する場合でもうまくはたらき、実用性が高いスケーリング手法です。変換式は以下のように書けます。
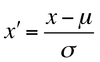
k近傍法で勝ち馬予測をする
機械学習アルゴリズムで最もシンプルな手法の1つk近傍法(k-nearest neighbors algorithm, k-NN)1による勝ち馬予測を例にスケーリングの有効性を示す実験を行います。ここでは勝ち馬を馬券内に絡んだ馬と定義します。
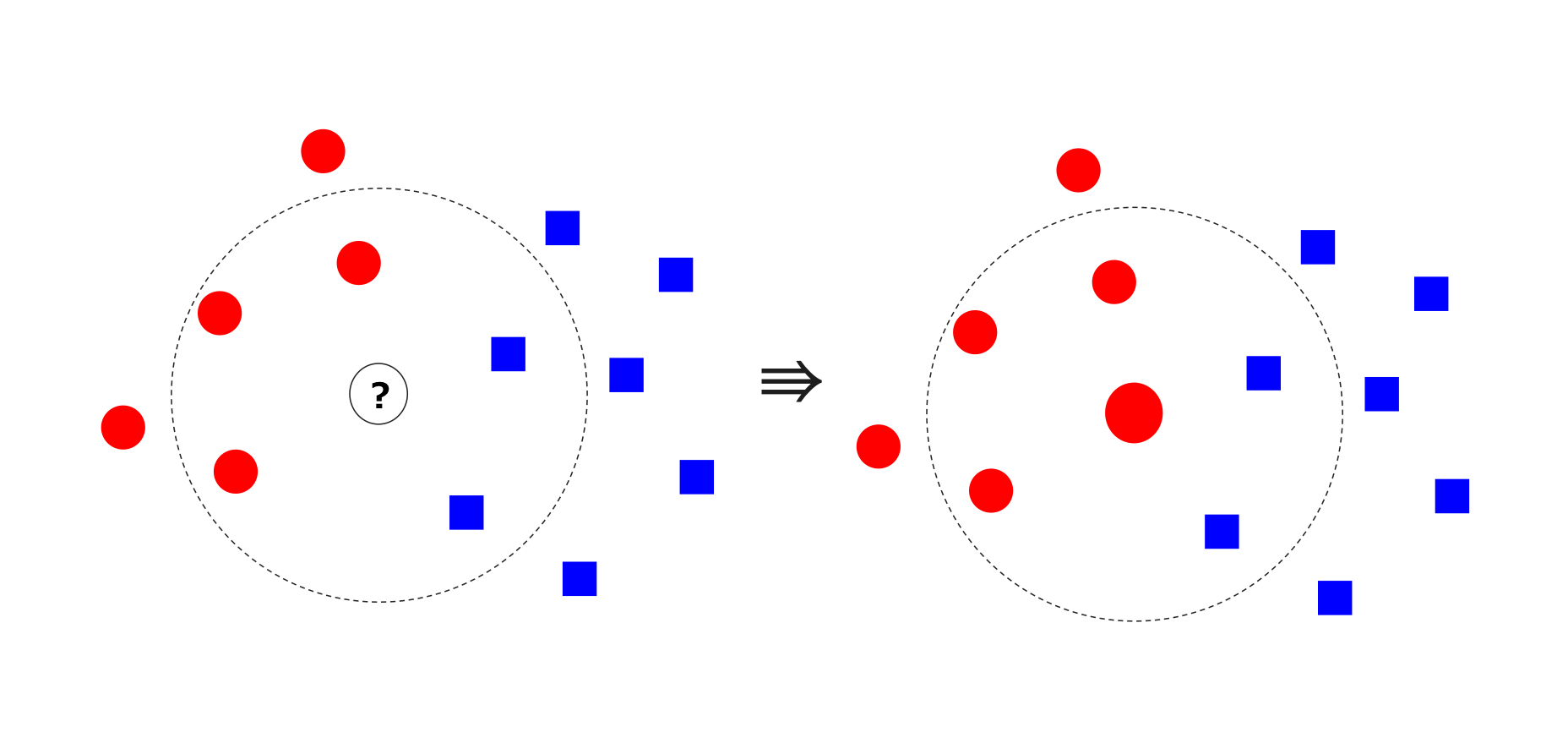
k-NNはクラスラベル(勝ち馬 or 負け馬)がわかっている学習サンプルと勝ち馬予測をしたいサンプルとの特徴ベクトルの距離を測り、k番目までの近くにあるサンプルで多数決をとり、サンプル数が多い方のクラスラベルを割り当てる単純なアルゴリズムです。以下の図における真ん中のサンプルが勝ち馬(赤)か負け馬(青)かを予測する例を考えます。k=5とした場合、真ん中のサンプルの近傍5つのうち勝ち馬3頭>負け馬2頭となるので、真ん中の馬は勝ち馬だと予測できます。勝ち馬になる確率を計算するときは、以下の例では3/5=0.6となります。今回はk=100で実験しました2。
入力データ
今回予測する対象の条件は、今週末に行われるフェブラリーSに合わせて東京ダート1600mの古馬戦に設定します。2015/1/1〜2015/12/31に行われた該当レース(48レース)を学習データ、2016/1/1〜2016/12/31(48レース)を評価用データとしました。また正例(勝ち馬)と負例の偏りが大きいと上手く予測ができないため学習データの負例を間引いて正例:負例=1:1になるように調整しました3。
特徴量は以下の8種類を使いました。
| 特徴量名 | カラム名 | 備考 |
|---|---|---|
| 馬齢 | age | |
| 斤量 | burden | kg |
| 脚質 | run_style | 逃げ=1, 先行=2, 差し=3, 追込=4 |
| 連対率 | win2_ratio | 馬の通算連対率 |
| 前走距離 | prev_length | メートル |
| 前走タイム差 | prev_time_diff | 1着との秒差 |
| 前走後3Fタイム | prev_last3f | 秒 |
| 前走本賞金 | prev_prize | 円 |
| 単勝オッズ | win_odds | 確定オッズ |
| 馬体重 | horse_weight | kg |
実際の入力データの中身は以下のように大小様々なスケールのデータが含まれています。
index age burden run_style win2_ratio prev_length prev_time_diff prev_last3f prev_prize win_odds horse_weight
0 4 57.0 4 0.100000 1800 0.1 39.3 1900000 2.7 484.0
1 4 57.0 3 0.100000 1600 0.7 35.6 0 26.2 558.0
2 5 57.0 2 0.066667 1600 0.5 36.5 0 17.2 494.0
3 4 55.0 2 0.153846 1800 1.4 40.9 750000 92.1 462.0
4 4 57.0 2 0.071429 1800 1.3 40.2 0 46.2 498.0
この入力データに対して標準化を適用すると以下のように特徴量ごとのスケールの異なりが解消されます。
index age burden run_style win2_ratio prev_length prev_time_diff prev_last3f prev_prize win_odds horse_weight
0 -0.350651 0.887719 1.344970 -1.069946 0.680274 -0.904699 0.346090 -0.013186 -0.707175 -0.010956
1 -0.350651 0.887719 0.248618 -1.069946 -0.189830 -0.345607 -0.204037 -0.370253 -0.435019 2.733302
2 0.510744 0.887719 -0.847734 -1.273420 -0.189830 -0.531971 -0.070222 -0.370253 -0.539249 0.359890
3 -0.350651 -0.398158 -0.847734 -0.741257 0.680274 0.306667 0.583982 -0.229306 0.328178 -0.826816
4 -0.350651 0.887719 -0.847734 -1.244352 0.680274 0.213485 0.479904 -0.370253 -0.203396 0.508228
評価
2016/1/1~2016/12/31(48レース)の各レースにおける勝利確率Top-1の単複的中率と回収率を示します。
| 単勝的中率 | 単勝回収率 | 複勝的中率 | 複勝回収率 | |
|---|---|---|---|---|
| k-NN(標準化なし) | 6.25% | 13.5% | 29.1% | 46.0% |
| k-NN(標準化あり) | 8.33% | 33.1% | 39.5% | 90.8 % |
標準化をすることで的中率と回収率が向上しました。回収率は100%超えていませんが、複勝回収率90.8%という数字は控除率が85%であることを考えると有益な予測が出力されていると思われます。単勝の成績があまり良くないのは、解いている問題が複勝圏内に来たか否かの2値分類であるためで、「1着になりやすい馬」と「3着までに入りやすい馬」の特徴が異なることを示唆しています。
続いて'16 フェブラリーSのレース結果とk-NNによる予測結果を示します。
▼ 着順と人気
| 着順 | 馬番 | 馬名 | 人気 |
|---|---|---|---|
| 1 | 14 | モーニン | 2 |
| 2 | 7 | ノンコノユメ | 1 |
| 3 | 4 | アスカノロマン | 7 |
| 4 | 5 | ベストウォーリア | 3 |
| 5 | 6 | ロワジャルダン | 6 |
| 6 | 13 | タガノトネール | 9 |
| 7 | 3 | コパノリッキー | 4 |
| 8 | 9 | モンドクラッセ | 10 |
| 9 | 16 | ローマンレジェンド | 13 |
| 10 | 2 | ホワイトフーガ | 5 |
| 11 | 10 | グレープブランデー | 11 |
| 12 | 11 | スーサンジョイ | 8 |
| 13 | 15 | サノイチ | 15 |
| 14 | 12 | マルカフリート | 16 |
| 15 | 8 | コーリンベリー | 12 |
| 16 | 1 | パッションダンス | 14 |
▼ 標準化なしk-NN
| 順位 | 馬番 | 馬名 | 予測確率 |
|---|---|---|---|
| 1 | 10 | グレープブランデー | 0.67 |
| 2 | 13 | タガノトネール | 0.67 |
| 3 | 7 | ノンコノユメ | 0.64 |
| 4 | 11 | スーサンジョイ | 0.64 |
| 5 | 14 | モーニン | 0.64 |
| 6 | 15 | サノイチ | 0.64 |
| 7 | 4 | アスカノロマン | 0.63 |
| 8 | 6 | ロワジャルダン | 0.63 |
| 9 | 9 | モンドクラッセ | 0.63 |
| 10 | 3 | コパノリッキー | 0.43 |
| 11 | 1 | パッションダンス | 0.41 |
| 12 | 2 | ホワイトフーガ | 0.4 |
| 13 | 8 | コーリンベリー | 0.4 |
| 14 | 16 | ローマンレジェンド | 0.39 |
| 15 | 5 | ベストウォーリア | 0.31 |
| 16 | 12 | マルカフリート | 0.2 |
▼ 標準化ありk-NN
| 順位 | 馬番 | 馬名 | 予測確率 |
|---|---|---|---|
| 1 | 4 | アスカノロマン | 0.71 |
| 2 | 14 | モーニン | 0.7 |
| 3 | 11 | スーサンジョイ | 0.67 |
| 4 | 7 | ノンコノユメ | 0.63 |
| 5 | 2 | ホワイトフーガ | 0.62 |
| 6 | 9 | モンドクラッセ | 0.62 |
| 7 | 5 | ベストウォーリア | 0.6 |
| 8 | 6 | ロワジャルダン | 0.57 |
| 9 | 3 | コパノリッキー | 0.55 |
| 10 | 13 | タガノトネール | 0.54 |
| 11 | 8 | コーリンベリー | 0.49 |
| 12 | 10 | グレープブランデー | 0.45 |
| 13 | 15 | サノイチ | 0.34 |
| 14 | 16 | ローマンレジェンド | 0.34 |
| 15 | 12 | マルカフリート | 0.28 |
| 16 | 1 | パッションダンス | 0.24 |
標準化なしの予測では上位が⑬タガノトネールや⑩グレープブランデーなど的外れな予測をしていましたが、入力データを標準化するだけで馬券内の3頭が上位4位までに入るという驚くべき結果に。④アスカノロマンは7人気ですから、単勝オッズだけを見ているというわけではなく、学習データの中にアスカノロマンと近い特徴ベクトルを持った勝ち馬が存在したのでしょう。ちなみにモーニンとアスカノロマンのワイドは1690円の配当でした。
おわりに
k-NNのようなシンプルなアルゴリズムでも、適切にデータの前処理を行えば十分に使えるレベルの予測器が作れます。逆に適切なデータ処理をしなければ、高性能GPUを積んでディープラーニングをぶん回したとしてもk-NNにすら勝てないショボい予測器ができるだけで、時間とお金の無駄となってしまうでしょう。発展的な機械学習アルゴリズムを試すのは、データを完璧に整えてからでも遅くはありません。
次回は予測モデルの種類とその評価方法ついて書いていく予定です。